在現有的橋梁（liáng）健康監（jiān）測係統，尤其是大（dà）跨徑的橋梁的（de）健康監（jiān）測係統（tǒng）中，用於采集數據的傳感器多達幾百甚至上千個（gè），有（yǒu）各（gè）種不同類型並（bìng）且分布在橋梁的不同測點，它（tā）們按照指定的策略獲取（qǔ）橋梁的響應信息，為橋梁結構健康狀態分析和（hé）評估提供數據基礎。在後續的橋梁健康監（jiān）測數據分（fèn）析中，由於存在眾多的傳感器類型和測（cè）點，如果（guǒ）不考慮不同數據之間的關聯性，不但會增加分析過程的複雜度還可能給分析（xī）結果帶來偏差，因此有必要對不同測點數據之間的關聯性以及不同類型（xíng）傳感（gǎn）器數據之間的關聯性進行（háng）分（fèn）析。

1 溫度（dù）與應變關聯性

對溫（wēn）度數據與應變數（shù）據的關聯性進行研究，首先需要對數（shù）據的（de）特征、數據的（de）分布、數據的變化趨勢以及數據之間的相關關係等進行觀察和分析；然後通過計（jì）算相關係數等定量指標來確定數據之（zhī）間相關（guān）性的強弱以及相關的方向；最後使用對應的分析模型對數據（jù）進行擬合，得出相應的擬合參數。

本文對溫度與應變的關聯性分析的步驟如下：

1）首先（xiān）將溫度數據和應變數（shù）據放在（zài）同一個折線圖中進行觀察，折線圖呈現的（de）是（shì）數據隨時間變化的趨勢，其中橫坐標是時間，兩個縱坐標分別是應變和溫度。如圖3-11所示是𝐷 = [63,0.5]的sn5測點應變數據與底板溫度數（shù）據隨時間變化的折線圖，從圖中可以看（kàn）出：a）經過數據標準（zhǔn）化操作之後，應變數據和溫度數據的數（shù）值（zhí）都（dōu）落在[0,1]之間；b）經過異常值處理和（hé）噪聲（shēng）去除操作後，溫度曲線（xiàn）與應變曲線變得更加平滑；c）數據（jù）標準化之後，溫度曲線整體呈正弦變化趨勢，應變曲線整體上也（yě）呈現正弦變化趨勢，且應變曲線變化趨勢和（hé）溫度曲（qǔ）線變化（huà）趨勢基本一致。對（duì）其他測點的應變數據與溫度（dù）數據進行觀察，能夠（gòu）得到類似的結果，這表明橋梁健康監（jiān）測（cè）數據中的應變與（yǔ）溫（wēn）度數據（jù）之間的相關程度較高，也說明在眾多影（yǐng）響（xiǎng）應變（biàn）的因素中，溫度是最主要的因素。

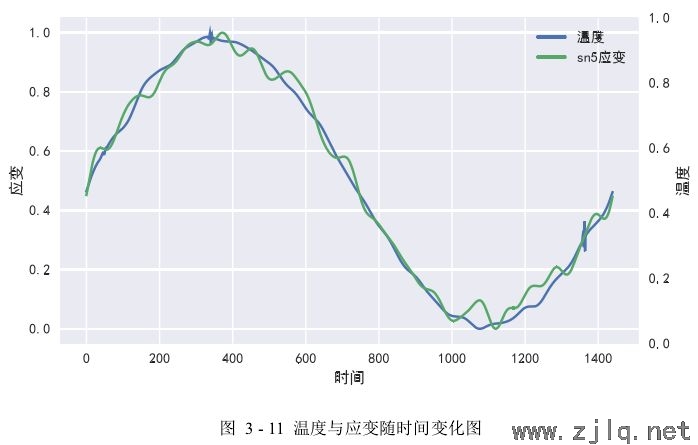
2）接下來使用相關圖對它們的相關形式、方（fāng）向和密切程度進行大致判（pàn）斷。如圖3-12 所（suǒ）示是𝐷 = [63,0.5]的 sn5 測點應變數據與底板溫度數據的相關圖，去除了時間（jiān）維度的（de）影響，隻關注溫度與應變兩組數據之間的關係（xì），其中溫度作為自變量放在橫坐標，應（yīng）變作為因變量放在縱（zòng）坐（zuò）標。從圖（tú）中可（kě）以看（kàn）出，溫度與應變具有相同的變化趨（qū）勢，當溫度增加時應變也相應增加，且二（èr）者對應的坐標點近似於分布在一條直線（xiàn）周圍，這表明溫度與應變（biàn）呈現線性（xìng）關（guān）係，並且根據坐標點的離散程度來看，它（tā）們具有較強的（de）線性相關性。

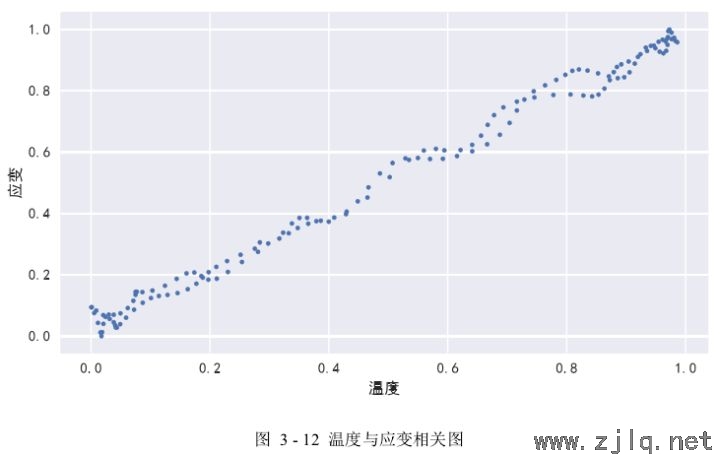
3）從前麵步（bù）驟可（kě）以得（dé）出溫（wēn）度與應變具有較強的線性相關性，這個線性相關性的強弱可以使用相關係數來衡量，相關係數是用來反映（yìng）變量之間相（xiàng）關性強弱的統計指標，其取值範圍是[−1,1]。如表3-1所示是工況𝐷 = [63,0.5]下 10 個測點的應變數據與溫度數據的相關係數表，從表中可以看出：a）預處理前和預處理後的相關係數都為正值（zhí），說明溫度與應變呈正相關關係；b）預（yù）處理後的相關係數基本都接近 0.99，根據相（xiàng）關係數（shù）絕對值越（yuè）接近（jìn） 1，相關性越強，說明預處理後的應（yīng）變數據與（yǔ）溫度數據具有非常強的（de）線性相關性；c）預處理後相關係數比預處理前的相關係（xì）數大，可見預處理後的應變數據與溫度數據的相關性變強，預處理提升了（le）兩者之（zhī）間的相關性，說明（míng）預處（chù）理操作（zuò）在本文（wén）的數據分析中起到重要作用。

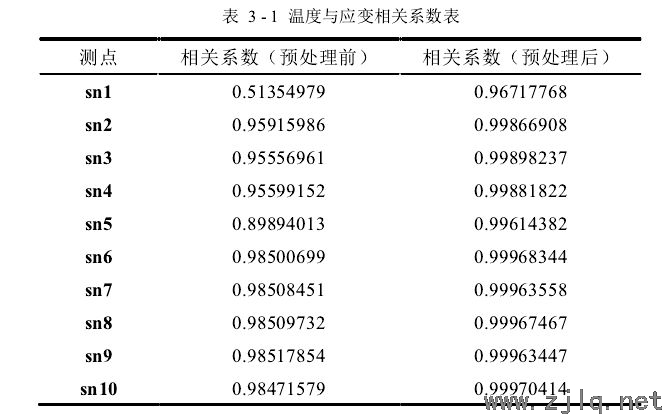
4）對於具有線性相（xiàng）關性的自變量和因變量，使用一元線性回（huí）歸模型進行分析，其數學表示（shì）形（xíng）式為：

𝑦 = 𝛼𝑥 + 𝛽 （1）

其中y是因變量，x是自變量，𝛼是回歸係數（shù），𝛽是常數項。要（yào）確定y與x之間的定量關（guān）係，需要確（què）定𝛼與𝛽的值，通常（cháng）使用最小二乘法或者梯度下降法來進行求解。而對於線性模型對數據的（de）擬合程度，本文使用均方根誤（wù）差（Root Mean Squared Error，RMSE）來進行衡量，RMSE 是模（mó）型估計值（zhí）與數據真實值之差的平方的（de）期望值的算術平方根，RMSE 的計算公式如下：

（2）

其中𝑓𝑖表示模型估計值，𝑦𝑖表示數據（jù）真實值。均方根誤差（chà）可以衡量模型對數據的擬合程度，RMSE 數值越小說明擬（nǐ）合越好。以𝐷=[63,0.5]的sn5測點應變（biàn）數據為例，使用一元線性回歸模型進行擬合分析，其中溫度（dù）數據作（zuò）為自變（biàn）量x，應變數據作為（wéi）因變量y，對模型進行求解可得到𝛼=0.96420992，𝛽=0.02618689，因（yīn）此溫度與應變的一元線性回歸模型數學（xué）表示形（xíng）式為：y=0.96420992x+0.02618689，該次擬合的均方根誤差為 0.029325，說明擬合程度較（jiào）高。

5）最後對所有測點進（jìn）行線性回歸擬合，並計算其均方根誤差（chà）。如表3-2所示（shì）是10 個測點應變數據與溫度數據擬合得到的回歸係數𝛼及常數項𝛽，以及對應的均方根誤差 RMSE。從表中數據（jù）可以看出 sn6-sn10 的擬合程度較高，sn1 的擬合程度最低，說明sn6-sn10 測點的溫度與應變的（de）線性（xìng）相關性較強，sn1 測點的溫度與應變相關性相對較弱。

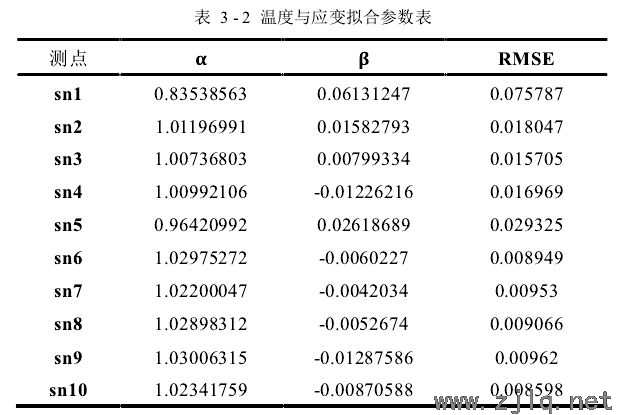
上述實驗可以得出：1）sn1~sn10 測點的溫度數據與應變數據都存在強線性相關性；2）這些測點的溫度數據與應變數據能（néng）夠使用線性回歸模型進行擬合，得（dé）到相應的回（huí）歸係數和常數項（xiàng）。

2 不同（tóng）測點應變關聯性

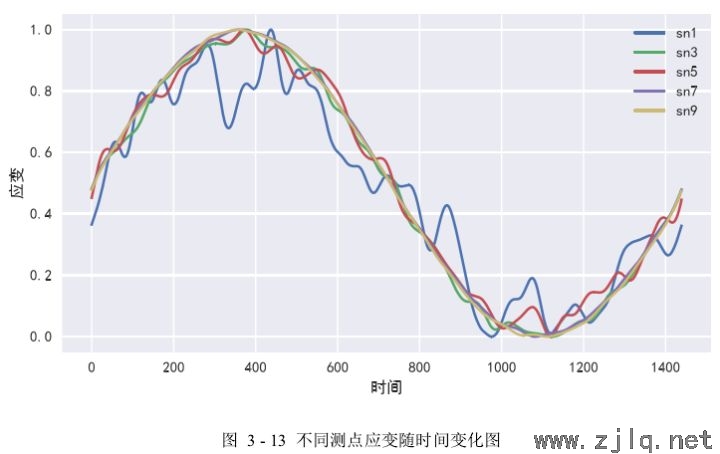
對不同測點之間的應變數（shù）據進行關聯性研究，首（shǒu）先需要對不（bú）同測點的應變數據進行定性觀察與分析。如圖（tú）3-13所示實驗中，從（cóng）工（gōng）況𝐷=[63,0.5]的所有測點中選5個（gè）測點（diǎn）：sn1、sn3、sn5、sn7、sn9，對這些測點應變數據隨時間變化的（de）趨勢進行觀察，從圖中可以看出五個測點的應變數據整（zhěng）體變化趨勢是一致的，都是呈正弦曲線變化，其中sn1測點和sn5測點的應變曲線波（bō）動幅度較大，而其他測點的（de）應（yīng）變曲線較平（píng）穩，由此可以說明不（bú）同測點的應變數據之間存在較強的相關性，但sn1測點、sn5測點與其他測點的相（xiàng）關性（xìng）相對而言弱一些。

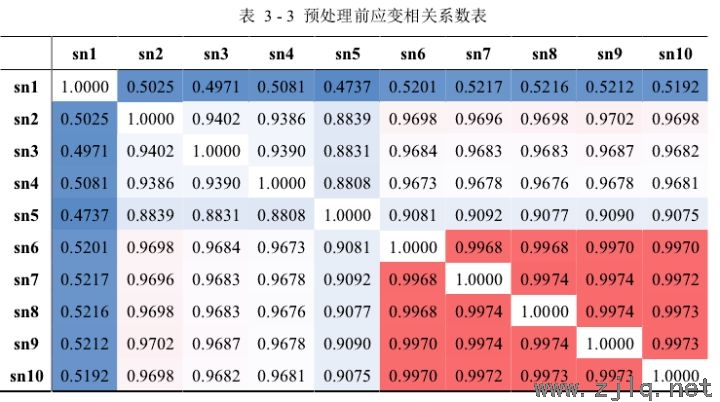
接（jiē）下（xià）來（lái）對定性的觀察結果做進一步的分析，分別計算不（bú）同測（cè）點應（yīng）變數據之間（jiān）的相關係數（shù）來定量地確定（dìng）它（tā）們之間相關性的強弱。如表3-3和表（biǎo）3-4所示實驗中，分（fèn）別計算預處理前後的應變數據之間的相關（guān）係數，並使用相（xiàng）關係數（shù）矩陣進行展示，表（biǎo）中數據使用不同顏色進行標記，其中紅色越深表示相關係數越大，相關性越強，而藍色越深表示相（xiàng）關（guān）係數越小，相關性越弱。

從表 3 - 3 實驗中（zhōng）可以得出：1）除（chú） sn1 以外的其他測點應變數（shù）據的相關係數在 0.9以上（shàng），表明（míng）這些測點（diǎn）應變數據的（de）相關性很強；2）sn6~sn10 測點應（yīng）變數據（jù）間的相關係數處（chù）於紅色區域，sn1~sn5 測點應變數據間的相關係（xì）數處於藍色區域，而 sn1~sn5 是橋梁（liáng）底板的測點，sn6~sn10 是橋梁頂板的測點，表明橋梁頂板應變數據間的相關性比橋梁底板應變（biàn）數據之間的相關性（xìng）更強。

從表3-4實驗中（zhōng）可以得出：1）所有測點預處理（lǐ）後的應變數據之間的相關係數變大，表明去除異常值和噪聲後的相關性變強，預處理操（cāo）作對應變數據的關聯性分析起了積極作用；

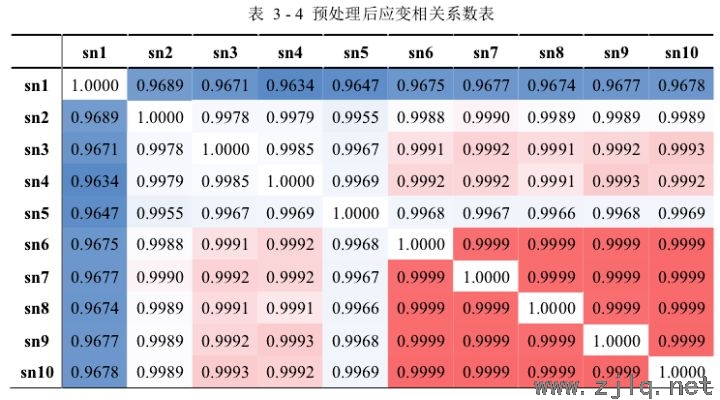
2）sn1 和 sn5 測點（diǎn）的應變數據與其他（tā）測點的應變數據相關係數增大到 0.96 以上，相（xiàng）關性大大加強，表明這兩（liǎng）個測點的（de）應（yīng）變數據對異（yì）常（cháng）值和噪聲比較敏感，更容易受到外界環境的影響。